| g e n u i n e i d e a s | ||||||
 |
 |
 |
 |
 |
 |
 |
| home | art and science |
writings | biography | food | inventions | search |
| halite fountain | ||||
| June 2021 | ||||
|
Heronis Alexandrini Spiritualium Liber 1583
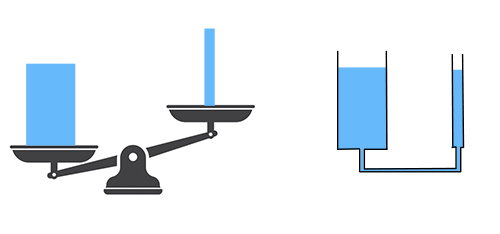
The ancient Greeks were polymaths, inventing everything from basic mathematical theorems, to automata, to early steam engines. They possessed a deep understanding of hydraulic and pneumatic engineering principles (though rarely converted this knowledge into practical devices). One of their more amusing inventions is known as "Heron's Fountain" which, after being primed with water, appears to run forever. This article explains how the fountain works, and demonstrates a far less well-known "Halite Fountain1" based on related principles. Hydraulic principles: Liquids and solids behave very, very differently. For example, the pan of a balance scale tilts downward under a heavy weight. No surprise. But consider liquids of the identical size and weight filling two containers connected via a pipe. They settle at the SAME height- "seeking their own level". How can the small tube of liquid balance the enormous weight of the much larger tank?
Solids are rigid, liquids flow. So if the large blue block teetered on its corner, all of the weight would concentrate on that point, and the scale would behave act exactly as if the block laid flat. But liquid would simply ooze into a pool, and must to be supported by a container. This container's walls carry away some of the forces. For example, I've chosen a lighter blue to indicate that portion of the water being supported by the container directly below (red arrows)- leaving only the two narrow columns of liquid above the pipe's entrance to balance their weight. Both columns are the same height and diameter, containing the same amount of liquid and thus balancing forces:
Imagine one surface of the container was lower than the other- water would flow sideways until level. If the dark blue column was now higher or lower than the surrounding liquid, liquid would flow to fill the gap. After a bit of sloshing back and forth, all surfaces are level and at the same height. The two narrow blue columns balance. This is a mechanistic, dynamic description of how fluids seek their own equilibrium and equilibrate forces when interconnected. After the fluids are no longer moving, we speak in terms of pressure uniformity within the fluid- Pascal's Law captures this physics, and is a key insight worth absorbing. But all we need to remember here is liquid levels readjust until the weight above each tube is balanced. How does Heron's Fountain work? (source) How can water from the lower level continually spurt into a higher stream? Doesn't this violate the laws of physics we just discussed? The explanation depends on two insights. First, is there a way to balance two columns of liquid in a "U" tube at different levels? The higher side will become the fountain stream. Normally, this arrangement is impossible as levels will adjust until the height of the liquid is the same in each arm (left-side of image below). One possible approach is to lower the density of the liquid in one arm- this leads to the Halite Fountain. But the other approach is to separate the two columns of liquid with a plug of air.
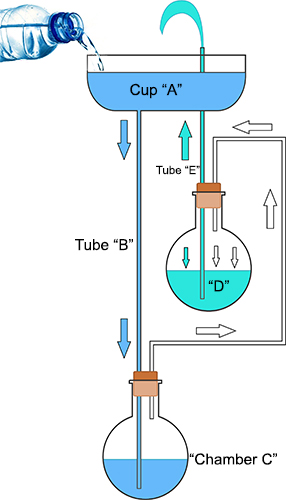
Since air is nearly massless its weight does not affect the column's height. In the right hand image the weight (and thus pressure) is the same on both arms of the U-tube, because the mass and area are identical. Even though the liquid level is higher. Of course, the slug of air is under pressure, compressed by the weight of the two liquid "pistons". If we suddenly removed some liquid from the right arm of the tube, air pressure would cause the remainder of that liquid to spurt out, like a squirt gun. Second, how do we create this air slug , and more importantly, allow liquid to apparently flow through the slug? The trick is to divide the U-tube into two compartments. In the first compartment water poured into Cup "A" flows down Tube "B" into air Chamber "C". As the water collects in the bottom of Chamber "C" it reduces the air volume, compressing the trapped air. This compressed air is routed to Chamber "D", whose bottom is filled with water. This is the water that will exit the fountain- not the water initially poured into Cup A. When water "D" is exhausted, the fountain will STOP!
Just like in the U-tube example, compressed air pushes on the water in Container "D", forcing it up Tube "E" until it emerges from the fountain. As long as Tube "E" is shorter than Tube "B", the air pressure in the tube is dominated by supporting the taller column of water Tube "B", and the air pressure is high enough for "E" to squirt out in a stream. That stream collects in Cup "A", keeping the level and pressure constant. The flow continues- for a while. But once Container "D" is emptied (see it lower in the film clip above) the fountain stops. You can reset and refill these containers, but it takes energy to lift the reset water into position, and it's easy to show that reset energy is the source of the fountain's *temporary* magical exuberance. The "trick" part of the fountain is familiar to any magician. It appears like one stream of water is circulating through the fountain. But in fact, there is a slug of air separating the path into two isolated tanks, and the apparent circulation is artful misdirection. The Halite Fountain: Unlike Heron's Fountain, the Halite Fountain is driven by a simple density difference. Less dramatic but still pretty amazing. Instead of air and one working fluid (typically water) there are two fluids. For example, water and a denser liquid containing a dissolved salt, such as table salt (the halite NaCl) or calcium chloride (the halide CaCl2). A "saturated solution"2 of CaCl2 is 40% denser than water! Imagine you hang a chain from one side of a pulley, and a rope from the other. The chain is much heavier per unit length than the rope. So, the heavier chain will pull the lighter rope up and over the pulley-- unless the rope is so long, its total weight matches the total weight of the chain. Then both sides will balance.
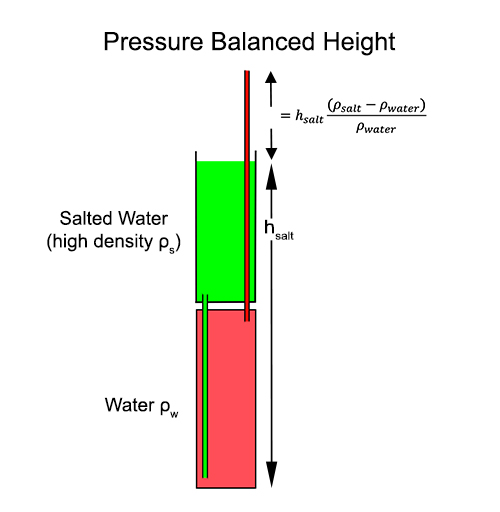
Now flip the image over, and imagine the chain and ropes are columns of liquid of two different densities. A taller column of the less-dense fluid is required to balance the pressure of the denser liquid in the shorter column.
The math to balance both columns is show in the figure below- we'd expect the water column to extend 40% higher than the CaCl2 surface. The Halite Fountain can be constructed out of two plastic bottles and some clear plastic piping. Bottle caps are typically molded from polypropylene, which is difficult to glue, so I friction-fitted the pipes into tightly drilled holes in the cap.
And here is the result of our experiment- the fountain runs for about five minutes until CaCl2 fills the bottom container, and water the top: (Note the lighter water floats on the denser CaCl2) Halite "fountains or springs" exist in the physical world, for example when sea water impinges on a fresh water aquifer. The sea water lifts up the fresh water, raising the water table. The height, in this case denoted by the Ghyben–Herzberg relation, is proportionately smaller because salt water is only 3% denser than fresh. As the earth warms and sea levels rise, salt water intrusion into our coastal fresh water supply is of increasing concern.
|
||||
|
______________________________________________ Although I independently (re)invented the Halite Fountain, Hero (Heron) of Alexandria proposed a related idea in the first century. Not a fountain, but a mechanism powered by two liquids of different densities. Hero was fixated on magic tricks- pitchers that turned water into wine, or fountains that flowed in the sun. If you scan through later Greek , German and Latin texts you can recognize an oil lamp which refills by pouring in WATER! TADA! That invention is illustrated in this 1851 translation by Bennet Woodcroft:
The upper and lower compartments initially contains oil, interconnected with two pipes as in our fountain. Water is heavier than oil, just like calcium chloride solution is heavier than water. When the oil wick at the right hand side is about to flame out after lowering the oil level in the upper bowl, simply pour water into the cup "D", which falls through pipe DAC to the bottom of the lower chamber. The heavier water forces oil into the upper bowl through the pipes EF, refreshing the sputtering wick. Oil and water only differ by 10% in density, so this approach would make a poor fountain compared to calcium chloride's 40%. Or even salt brine at 20%. Oh yes, Heron's Fountain is on page 55 of the Woodcroft translation, and here in the German.... 1 My terminology, chosen to emphasize the salt solution, and for alliteration with "Heron". Halite or Halide depending on salt. 2 A "saturated solution" means water contains the maximum amount of the salt in solution. Practically speaking, you continue adding CaCl2 to water until no more dissolves, and a white powder accumulates in the bottom of the container. Note CaCl2 and water participate in an exothermic reaction and will become quite hot- so add the CaCl2 slowly to ice water and stir. Instead of tossing used brine down the sink, I save the leftover liquid to deice sidewalks in winter. An even larger density difference is obtainable with mineral oil instead of water for one fluid, and saturated calcium chloride for the other. Also, these two liquids are immiscible so can be re-used indefinitely. However, if the oil's viscosity is too high the fountain will not spurt- low viscosity mineral is acceptable. Note oil and saturated calcium chloride make a great U-tube demo |
||||
Contact Greg Blonder by email here - Modified Genuine Ideas, LLC. |