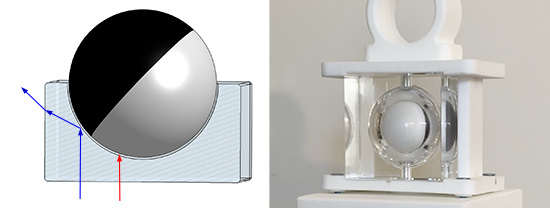
(the Lunase CONIC carriage clock prototype)

Albert Einstein is reputed to have said "Everything should be made as simple as possible, but not any simpler". Because simple things, while easy to realize, are sometimes misleading.

For over two thousand years humans attempted to replicate the moon's phases with gears and cams. They knew the earth and moon were spherical, so the easiest, simplest solution, was to fabricate a black and white hemisphere which rotated once per lunar month. A moon, in miniature.

Problem solved.

One of the earliest examples of a hemispherical moon is the astonishing Antithykera astronomical computer, dating from ~200 B.C.E. Seen in this computer simulation:

Followed by countless intricate table-top orrerys, and even wrist watches:

(Arnold & Son "Luna Magna")

Unfortunately, these "simple" analog computers all share a common problem- the apparent lunar phase depends on the viewing angle! When you look at a sheet of paper from different directions, the image only changes perspective, but you can't see around the paper, so the images are basically the same at any angle:

When you look at the identical point (the red dot) in three dimensions, however, different sides of the hemi bi-sphere are revealed:

Which is patently obvious in this carriage clock:

One solution is to abandon the third dimension and switch to planar displays. We discuss the history of flat lunar displays on our Lunase page. Sadly, even simple flat displays create attractive, but unrealistic renditions of the lunar phase (though our Lunase design addresses most of these concerns, albeit with a bit of additional mechanical complexity).

Perhaps there is a away to add a dash of optical complexity, and somehow "flatten" the sphere's image so its appearance is independent of viewing angle? In other words, is there some kind of "magic lens" which bends the light so both viewing angles terminate on the same point of the hemi?

Such "magic lenses" exist- basically a slab of fiber optics bundled tightly together- a "Fiber Optic Plate" (FOP). Each fiber acts like a dedicated narrow pipe, carrying an image from just above the top surface to just below. The above sketch is idealized and frankly, physically impossible. In optical science each ray's path must be unique and reversible in time. In this illustration a ray from the hemi, passing though the lens and emerging from the top surface can travel in either the green OR blue direction- so impossible.

More realistically, a a bundle of rays enters the fiber, rattles around and emerges from the other side like water from a garden spray. The spray angle is called the "numerical aperture". Minuscule changes in viewing angle send the rays bouncing around almost randomly within this cone, such that each entrance ray has a unique exit ray:

Clearly, these rays will average over the hemi's surface and blur the image. This glass FOP plano-concave block illustrates the point:

Blurring becomes unacceptable when the gap between FOP and hemi is more than a mm or two. So instead of a flat magic lens perced above a sphere, we must fabricate a hemispherical pocket of nearly the same radius as the hemi, and in so doing, maintain a constant air gap. The closer the better.

Problem solved?

Not quite. The air gap between FOP and hemi will distort the image, particularly resulting from total-internal-reflection when the light ray hits the air gap at a shallow angle. The RED ray passes almost directly through the air gap- the shallow angle BLUE ray bounces off, vignetting the hemi image as seen through this clear acylic lens:

Fortunately, there are two practical solutions. We can fill the air gap with a liquid that matches the index of refraction of the FOP,

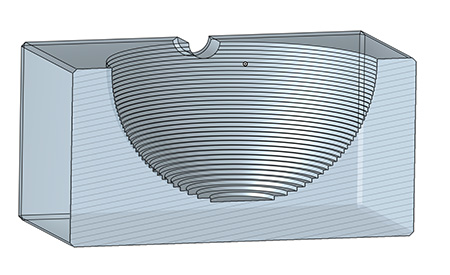
optically "erasing" the interface. Sealing the hemi within a FOP cube, while allowing the hemi to rotate in a clear liquid is a challenge, but a surmountable one. Here is a quick prototype illustrating the principle in a wrist-watch format:

Alternatively, we can avoid the messiness of liquids by locally designing the surface of the FOP hemispherical pocket to avoid shallow angles and total internal reflection. Here, we simple replace the smooth FOP's hemi pocket with a stepped profile, cut on a diamond-tool lathe.

Each ray now encounters a flat, rather than curved, surface and passes straight through the air gap

The net effect is magical:

and a huge improvement over a naked hemi:

To accurately mirror the lunar cycle:

A few mechanical details:

• A commercial, battery-operated lunar clock mechanism connects to the hemisphere via an axle supported on ball-bearings. These inexpensive plastic-geared clocks are quite fragile and under-powered, so friction minimization is critical.
• The cube containing the clock face can rotate around the base.
• The clock face is simply a wrist watch mounted in a removable plate.
• The hemi is centered in a transparent cube made from two plano-concave lenses. The front lens is a plastic FOP, and the rear clear acrylic.
• To set the lunar phase simply rotate the base, and the hemi follows. An annular steel ring in the base holds a magnetic catch in place, locking down the lunar phase setting.
• In the case of an index-matched plano-concave lens, the axle enters the glass cube via a magnetic feed-though. This seals in the oil with longer life and minimal friction compared to o-rings. A bellows expansion chamber accommodates thermal expansion- the chamber can be hidden in the hemi. An oil-filled glass hemi is under construction.

• The large plastic and glass FOPs were sourced from Incom.
• The wrist watch glass FOP from Schott.
• Bern Optics fabricated the glass FOP wristwatch plano concave lens.
• Incom fabricated the glass FOP carriage clock plano concave lens.
• Greenlight Optics machined the stepped plastic FOP lens.