| g e n u i n e i d e a s | ||||||
 |
 |
 |
 |
 |
 |
 |
| home | art and science |
writings | biography | food | inventions | search |
| it's just a phase | ||||||||||
| Jan 2022 | ||||||||||
|
With the advent of mechanical timepieces, these natural rhythms were tamed and regularized. Today, watches are an indulgence made redundant by ubiquitous time displays on phones, thermostats and microwave ovens. Still, as a token of the past and a paean to human ingenuity and artistic expression, clocks fulfill a special calling. From the early 17th century onward the lunar cycle appeared on tall case clocks. Historians claim the mechanism helped foretell the tides for fishing, or anticipated the light of a full moon for safe travel at night. The mechanism was simplicity itself- a rotating disk containing two moons peeking out of a window framed by two half-circles. These half-circles occlude the rotating waning moon, or reveal, on the opposite side, its rise. Mimicking the lunar cycle, the disk rotates once every 29 days, with only rough astronomical authenticity. How do these clever occlusion wheels fail to capture reality? First, the "terminator", that hazy line between dark and light on the lunar surface, is really an arc of an ellipse extending from pole-to-pole. Astronomically, the sun hits the moon and fully illuminates one side, casting a great latitudinal circle between the poles. As the moon orbits the earth we view this circle at an angle- and a circle seen on edge is an ellipse. An accurate1 lunar cycle is captured below in this sequence of images. Note how the terminator runs pole-to-pole and reverses curvature from waning to waxing:
But unlike a true lunar phase, the occlusion disk mechanism simply nibbles away at the rotating moon's image - never spanning from pole to pole until the moon is fully covered. Never changing in curvature. Never a straight line at quarter-moon Most lunar watches implement miniature versions of the tall clock "double bosom" occlusion mechanism. Sometimes, by expanding the gear train, they tick out a more accurate lunar cycle of 29.53059 days (slipping by a day once every century or so). Even so, these modern lunar watches remain infested with mice, nibbling away at the corner of a moon made from cheese:
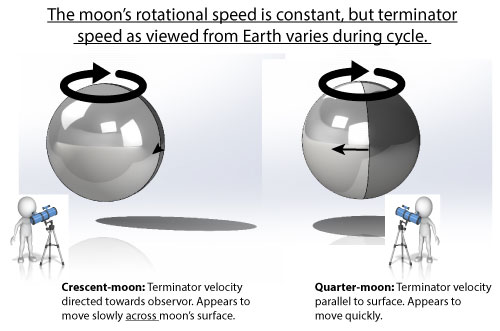
There is also a subtle error in the display's rotation. The moon-wheel is driven at a constant rate, but the speed of the terminator across the moon's surface varies sinusoidally in time2 (a consequence of projecting the rotating circle of the illuminated moon in the direction of the Earth). This illustration offers a qualitative explanation:
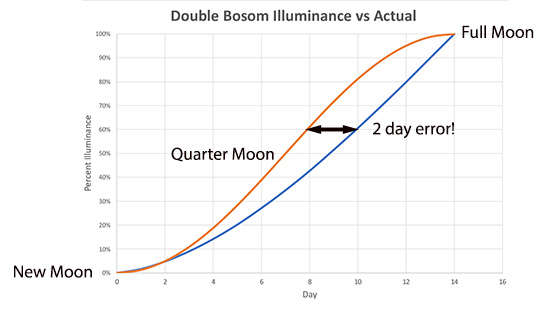
As the terminator is revealed around the time of a full or new moon, the crescent's velocity is aimed directly towards the observer, and not parallel to the surface. Just like a car barreling straight towards you appears at rest, the fastest terminator velocity occurs at a quarter moon when it is racing across the field of view, and the slowest at the thin crescents when it is aimed in your direction. In this graph, we compare the percentage of the illuminated moon surface (blue curve) for the double-bosom disk versus the actual sinusoidal behavior (red curve). Note the two are out of sync by nearly 2 days during part of the cycle! Somewhat diminishing the ostensible value of a gear train promising a century of accuracy3....
Finally, the terminator cusp-to-cusp angle relative to the horizon appears to oscillate throughout the day due to the 23.5° tilt of the Earth's axis changing your perception of "up" relative to the lunar ecliptic. This is the parallactic angle. In the northern hemisphere, the Moon will appear tilted to the left at moonrise and to the right at moonset. When it transits (crosses the meridian), it’ll be roughly vertical. No lunar watch even attempts to replicate the daily parallactic cycle. Now there are dozens of ways to imagine a more accurate lunar phase module. Perhaps based on ferrofluids, moiré patterns, silicon MEMs devices, lenticular screens or a miniaturized orrery. Realistically, many of these designs demand excessive power for use in a wrist watch, or suffer from shock or maintenance problems. Ideally, an improved lunar phase mechanism would solely rely on traditional planar watch technology for ease-of-design and manufacture. We decided to pursue three approaches. This article investigates a planar phase mechanism inspired by the nested wheels of a day/date complication, as well as the iris from a mechanical camera. But we have also built a novelty clock LUNASE REFLECTIONS where the moon floats above the clock as a real image created by reflections off of a pair of parabolic mirrors. Based on the toy witha floating frog. And a third approach, the Lunase CONIC, utililizing fiber-optic technology.
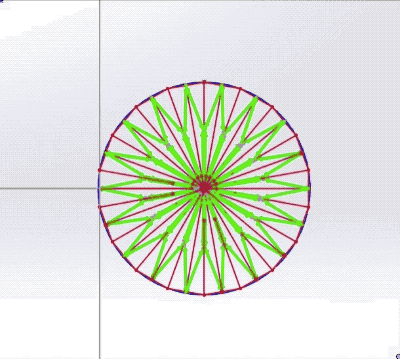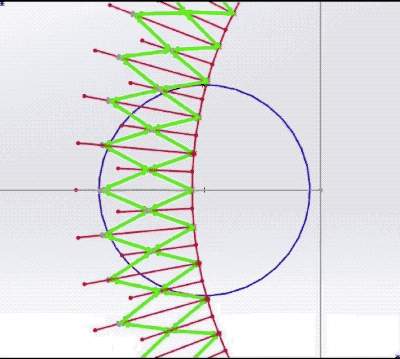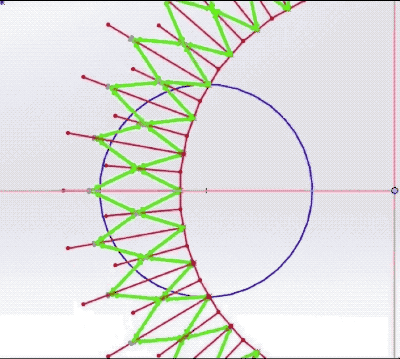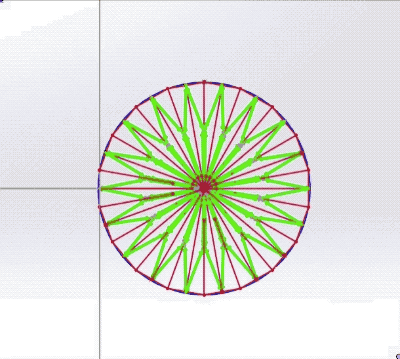
The "Lunase" concept consists of an asymmetric iris consisting of six partial wheels, each carrying a segment of the terminator. These semi-circular arcs pivot on bearings in a synchronized manner to approximate the time-varying shape of the terminator's ellipse.
Not shown in the above simulation are the individual segment's driving gears or the fly-back mechanism that resets the wheels at the end of a lunar month. A modified spiral cam may combine the fly-back function with an exact sinusoidal terminator speed. The red cam at the top of the image is a standard Archimedes spiral, causing the follower arm to rise at constant speed. The green cam has a sine wave impressed on the spiral (in the actual clock mechanism, a related curve, abs(cosine), drives the rack and pinion through a full lunar month). A practical implementation might employ planetary gears. This video illustrates the approach with a skeletonized gear train and then a more compact mechanism replacing pivoting gears with slotted racks. The edges of each annular ring are emphasized for clarity (giving the crescent moon the appearance of a "croissant"), but would be less noticeable in reality: A "fast" mode is also desirable, where a button press can replay the entire lunar cycle in thirty seconds. One detail is worth mentioning. The terminator's edge will be faceted due to the small number of segments. We suggest printing a gradient on the wheels instead of a sharp interface between black and white (a trick used in the Midnight Planetarium and the Krayon Everywhere). Not only is this more realistic, but will fool the eye into thinking the terminator is a smooth arc, even if the overlap is poor as shown in this exaggerated example:
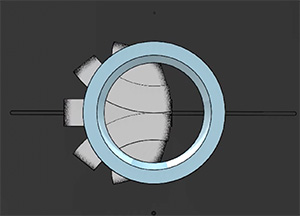
A few preliminary image wheels: I've fabricated a desk clock, using off-the-shelf and 3D printed gears, as a proof-of-principle. The gear train visible on the clock's front converts the hour hand's motion to a lunar month. In this prototype a simple quartz battery clock drives the hands. Though a relatively weak power source, the second hand is geared-up by a factor of 2,551,392 (approx. the number of seconds in a lunar month), and manages to smoothly operate the phase mechanism. The moon viewed from the Northern Hemisphere:
Hand operation of mechanism. In this model the sweep of the moon's terminator (from left to right) is as-viewed from the southern hemisphere. The largest gear in the lunar train contains a ratchet mechanism, allowing the phase to be set independent of the time, and the middle vane protrudes left/right to indicate waxing/waning: And the Lunase clock with night sky anodization and luminous hands:
|
||||||||||
|
Footnotes and Additional Details
Other approaches: There are hundreds of moon phase watches on the market, too numerous to discuss in detail. But a few notable examples include the original perpetual calendar watch of Thomas Mudge circa 1765, Arnold & Son's Luna Magna with a rotating marble analog moon computer, the Richard Lang Terraluna with a map of the Earth, the sun and moon in planetary alignment, and the Ochs und Junior watch with a carefully designed slot to occlude a traveling disk. The Ulysse Nardin Moonstruck rotates a lobed terminator behind a round window (simulated by me in red). This arrangement comes closer to an accurate representation of the terminator's speed and shape, but is still not pole-to-pole and the orientation of the lunar poles changes throughout the month.
A pantograph version, fabricated using MEMs technology or very fine machining skills, *is* possible. However, unlike the Lunase arced disk approach, this pantograph iris does not "rise" correctly. That is, the new crescent should always appear on the same side of the moon (in the same way the sun always rises in the East), but with this pantograph the rising alternates between East and West. A more complex pantograph mechanism can remedy. Very steam punk, though.
A sliding rack complication could power a central vane in addition to annular rings. Taking into account the nearly invisible polar edges of the new crescents, this approach is a close match to an ellipse:
Rack and pinion gearing drives the rings: A full set of horizontal vanes can accurately reproduce the elliptical terminator, though may suffer from greater friction. Here we illustrate a co-linear stack of pinions driving an array of horizontal rack vanes, but a stacked pulley driving an array of belts would work as well. The pulley stack diameters are proportional to the square root (1-d^2), where d is the distance from the center of the stack to the pulley. The stack is elliptical in outline. For simplicity, this proof-of-concept wraps a continuous string around two elliptical fusees impressed by a spiral groove, but has to be rewound at the end of each lunar cycle. Also, the band might slip over time and lose synchronization:
Alternatively, a chain or perforated belt could run over toothed pulleys, assuring perfect sync. The belt lengths could be individually selected so an even number of pulley rotations returns them to their initial state- thus no flyback mechanism would be required. This approach employs loops of roller chain, carefully designed so each band (there will be 15) has an even number of alternating white/black regions so they line up in sync as the crank is turned. Crude proof of concept.
1 Crescent moons are widely portrayed by artists, often in absurd flights of fancy. For example, some claim stars are visible through the horn (and presumably visible though 3,000 kms of lunar rock). A conceit repeated in many watches:
2 For additional motivation, I measured (blue curve) the width of the illuminated surface in the lunar phase montage at the top of this page, then calculated the illuminance. Note the reasonable fit to a cosine (in orange):
Most readers from the EU/US tradition are surprised to learn the average angle of the terminator depends on latitude! We just assume, based on our own observations and the "classic" image of the moon in art and popular culture, that the moon's crescent is always nearly vertical. But residents of Chile would disagree. I hope watchmakers will offer a Lunase model customizable to the client's home latitude.
3 There is an old saying that even an unwound watch is accurate twice a day. The fact is, only the AVERAGE length of a (synodic) lunar month is "29 days, 12 hours, 44 minutes and 3 seconds". How important is a gear train that exactly matches this average? Because of subtle interactions between the earth, moon and sun's elliptical orbits (along with their tilted orbital planes) a lunar "month" might vary by 10 hours from cycle to cycle. Almost half a day! And the angle of the poles with respect to your viewing latitude varies daily. Absolute verisimilitude is a lofty goal... |
||||||||||
Contact Greg Blonder by email here - Modified Genuine Ideas, LLC. |
||||||||||