Before using this nitrite curing calculator, please read this article on nitrite curing safety

If you are looking for our salt brine calculator, click here
As a rule of thumb, since Prague powder is mostly salt
no need to additionally salt brine when curing.
Not applicable for sausages and other ground meats
Make sure to pay attention to the units!
Reload page to erase and start over
Use at your own risk....

NOTE: During cooking the heat will speed up diffusion. So if the calculator predicts 10 days, even after six the nitrite will make it all the way to the middle during cooking. So OK for color. BUT, salt is also rushing in late, and salt does its best job early in the cook by breaking down muscle fibers and grabbing onto water. So best to wait the full time.

(If cure time is longer than 10 days, consider injecting the brine to speed up the process. If you inject every inch or so, then input two inches in the calculator meat "thickness" to estimate the cure time. But the actual time depends on how much brine you inject, uniformity of injection, etc..)

You might wonder why the projected cure time is around half as long for a cylinder of meat, as compared to a flat slab of the same thickness. After all, to reach the center, salt has to travel the identical distance from the surface.

And you are partly correct. The first few salt ions end up in the center at around the same time. But when curing, we care more about the time for the entire hunk of meat to fully saturate with salt, rather than how long it takes for the first ion to cross the "finish line".

Surface to volume matters. In a wide slab of meat (e.g. a brisket, ignoring the ends), salt mostly enters from the top and bottom. But in a cylinder or square cross-section (e.g. a tenderloin), salt enters from FOUR sides, and thus saturates the meat twice as quickly. Think of a sports arena: if you only open the East and West gates, the stadium fills half as fast as when you also unlock the North and South. True, a few fans reach their seats on the field just as quickly in either scenario, but there is a factor of two difference in time filling the entire stadium.

The stadium is merely an analogy, here's the science.

Heat, salt ions and food dye all move through a solid by diffusion. The salt ions do not "sense" there is a large hunk of unsalted meat in the center and are "drawn in" to fill the void. Instead, they simply randomly bounce around, driven by thermal fluctuations, eventually stumbling into the center. And stumble out- they wander aimlessly into every nook and cranny. Eventually, this random walk uniformly fills the entire slab of meat, erasing any evidence of the unsalted meat.

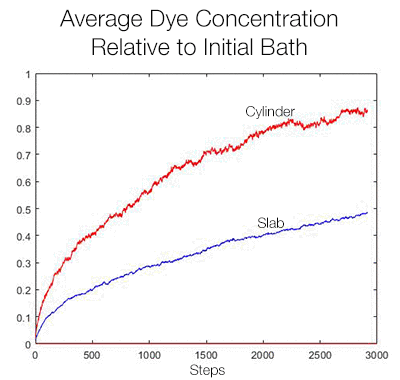
In this 2-D simulation, the frantic red dots represent salt ions randomly walking into either a rectangular slab of meat, or a cylinder. There are only 40,000 ions in this simulated cross-section, so the boundary between salted and unsalted meat is rough. In a real salt bath, there are over 10²⁶ salt ions, and the boundary is smooth.

Note how the cylinder fills in before the slab (in practice, cooking heat evens-out any irregularities in the salt concentration, and you can often stop brining when you are close to 80% of the desired final salt level). And how the corners of the slab (where salt arrives from two directions) saturates quickly. It's the same reason the corner of a steak overcooks and turns gray.

This plot calculates the average salt density vs time for the rectangle and circle (normalized to the original salt density in the bath). The red curve is the average salt density in the circle, the blue curve the average salt density in the middle half of the rectangle (to ignore the effect of salt entering from the ends).

Clearly, the circular cross-section fills in around twice as fast as the slab.

While these simulations are suggestive, we can also perform a simple experiment (which you can replicate at home). Dye molecules substitute for the salt ions, and slabs of molded gelatin, for the meat. A 6"x6"x1" slab of clear gelatin was placed in a bath of green food coloring, along with a 6"x1"x1" rectangular bar and a 1" cylinder. Every couple of days they are removed from the bath, a sample is cut with a knife (away from the edges) into 2mm thick cross-sections and then photographed.

Again, the cylinder or square are darker and more uniform, filling with dye more rapidly than the large slab. Dye molecules are similar in size and shape to herbs and spices- as you can see, it takes at least a week for their flavor to reach the center of a one inch thick hunk of meat (or many veggies). Which is why spice rubs merely deposit their flavor goodness on food surfaces

(BTW: the perimeter appears dark green because the camera images the top of the slab along with the green outer sides of the 2mm thick sample. If you cut the gelatin into paper-thin sections this dark band disappears. But cutting floppy gelatin is problematic without a jig, so we decide it was easier to to use 2mm slabs).