| g e n u i n e i d e a s | ||||||
 |
 |
 |
 |
 |
 |
 |
| home | art and science |
writings | biography | food | inventions | search |
| all thumbs | ||||||||
| Feb 2016 | ||||||||
|
One of the greatest of all cooking challenges is knowing when food is "done". Sometimes a thermometer is your best friend- especially for cuts like steaks or white meat chicken breasts. Or pork tenderloin. In these cases, a mere 5 degrees F separates tender from tough. No amount of pressing on the surface and watching it rebound, or divining juices for color is as accurate as a good digital thermometer. Alternatively, for baked goods weighing food is often the best strategy. However, even if you learn to reliably separate "done" from "oops", predicting cooking time is equally valuable. Otherwise, the green beans are ready an hour before the rib roast has rested, and no one wants to eat soggy limp green beans. Perhaps a "rule of thumb" exists, one that is accurate and predictable under all conditions. Like "30 minutes a pound" or "5 minutes an inch for medium rare". And these rules do exist. Equations to accurately predict1 how fast a slab of aluminum will heat in an oven are easy to derive and well known- something along the lines of:
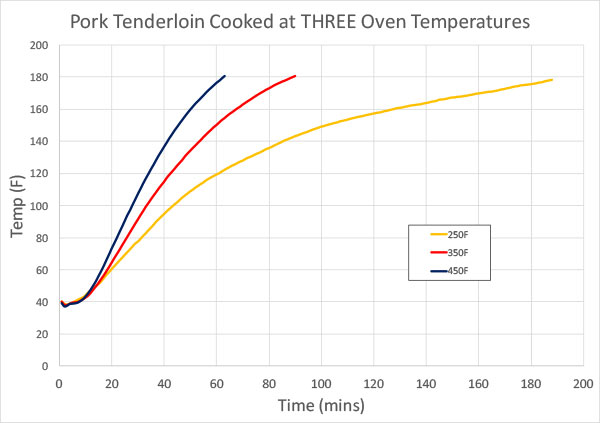
(where L is the distance to the center of the slab, Traw is the unheated starting temp, and D is the thermal diffusivity) The problem is, food cooks very differently than a lump of inert aluminum. Food not only heats up in an oven, it also evaporatively cools. While the above equation correctly predicts aluminum will eventually reach the oven's temperature setting, food never rises above the boiling point of water, 212F. In fact, moist food can stall and plateau at 150F for hours when cooked low and slow! Plus, food oozes delicious juices and fat, shrinks as collagen hydrolyzes and turns into gelatin, and is surrounded by a bubble of moist, insulating air whose size depends on airflow and oven proportions. Can you predict cooking times in the face of these real-world complexities? Absolutely, though it takes considerable computing power, a mix of rigorous and heuristic modeling, and lots of accurate data. Unfortunately, few rules of thumb emerge from this more detailed analysis. Alternatively, tables or graphs based-off actual cooking times are sometimes the most practical solution. For example, here I've cooked pork tenderloins at three different oven temperatures (each tenderloin about 2.5" thick weighing 1 lb) :
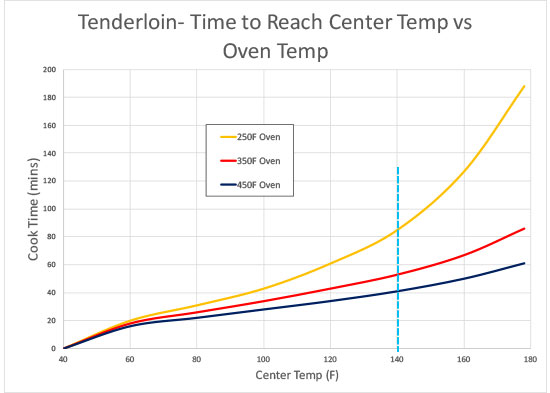
In the first 10 minutes of cooking, heat is diffusing from the oven to the center of the tenderloin. Thus the delay in temperature rise. This delay is almost independent of oven temperature. The curves are similar and roughly exponential after the first few minutes of baking. But even exponentials are problematical as rules of thumbs. For example, there is a larger gap between the 250F/350F curves than the 350F/450F curves, and the relative gap grows at higher temperatures. So any simple rule of thumb is suspect. Another way to view the same data is to flip the chart around, and ask, for a given desired internal temperature, how long will it take to cook in different ovens? In other words, how long until it is "done"?
For example, pork tenderloin is perfect around 140F (yes, it is pink, but will coast to 145F before serving and that satisfies the USDA for safety). The blue dotted line indicates it takes:
To cook dark meat chicken of the same thickness (say a rollatini), 180F-190F is best:
Note the huge time penalty cooking at 250F- almost 175% slower2 than at 450F. Why would anyone accept this time penalty to cook a simple hunk of meat? The reason is uniformity. The hotter and faster a thick piece of food cooks, the greater the difference in temperature between the surface and center. When 5F matters for tenderness, a low slow cook followed by quick sear to brown and flavor the crust, is often the best strategy. Otherwise the outside is tough, while only the center remains tender. What about the dependence of cook time on thickness? Well, again real-world data trumps simple rules of thumb. Although a " diffusion equation" inspired rule predicts the time grows in proportion to the thickness of the food "squared", in reality that rule breaks down below an inch or so in thickness. Not bad above, except in low and slow cooks when the meat loses 30% of its initial weight.... So what is to be done? Well, I'm accumulating a compendium of data taken over multiple cooks and in multiple ovens, and using this data as the basis for a cook-time prediction tool based on a little theory, and a lot of interpolation. Stay tuned for more details. And we will be looking for volunteers to help validate the predictions- there is only so much meat I can eat in the interest of kitchen science.
|
||||||||
|
--------------------------------------------------------------------------------------------------------
1This equation is most accurate when applied to high diffusivity materials, where there is little delay between heating the surface and interior. By adding a time delay to the equation (e.g. around 10-15 minutes in the case of 2.5" diameter tenderloin), the accuracy is improved. More precise treatments are based on some modification of a complex error function. 2The energy content of air is proportional to its temperature. But not measured in degrees Fahrenheit, which selected 32F as the arbitrary location for the freezing point of ice. Instead, scientists use the Kelvin scale, where 0K is absolute zero -- the point where classic atomic motion ceases. On the kelvin scale, 250F=394K, 350F=450K and 450F=500k. Thus one might expect food in a 350F oven cooks 15% faster than in a 250F oven, and food in a 450F oven cooks 11% faster than in a 350F oven. Which is close to what we measure for a "done" temp of 80F. But at 180F, where evaporation is more relevant, the proportions are 55% and 30%. Go figure. |
||||||||
 Contact Greg Blonder by email here - Modified Genuine Ideas, LLC. |